How Can Magnetic Monopoles Exist (and what good are they)?

This is kind of a weird one, I'll admit, but it's something that's confused the hell out of me ever since I read somewhere that magnetic monopoles were theoretically possible.  Both the occasional-scientist (the "how do they exist?" part of the question) and full-time engineer (the "what good are they?" bit) parts of me are pretty intrigued by the whole idea, which seems to violate everything I know about electromagnetics. 

For people with lives, the concept of a magnetic monopole is pretty simple.  Any magnet, from those giant ones on cranes at junkyards to the tiny little bits on your hard drive, has both a north and a south pole.  As all kids who grew up in a house with a refrigerator (if you didn't grow up with a refrigerator, my apologies and that totally sucks by the way) know, two magnets will push each other apart when two of their like poles get close to each other, and stick together if two opposite poles come into close contact.

A magnetic monopole is basically a chunk of material with only one magnetic pole, which means all sides of it would exert the same type of force on another magnet regardless of what part of the monopole the other magnet was close to.  A good analogy would be two styrofoam balls with a positive electrical charge; they're going to do the same thing (repel each other) no matter which way you bring them together.

The big problem with magnetic monopoles is that, according to classical physics, they can't exist.  Gauss' Law of Magnetism (sort of the Rodney Dangerfield of Maxwell's equations) says (among other things) that the net magnetic "charge" in an object is always zero, meaning that if part of the object is positively magnetized, some other part has to be equally and oppositely magnetized.  In other words, you can't have a magnetic north pole without a magnetic south pole.  This is easy to test if you don't mind breaking stuff: just take a magnet and crack it in half (see figure below).  You'd think what that would do is make a pair of opposite monopoles (one magnetic north and one magnetic south), but what actually happens is that the electrons in the two pieces reorganize themselves to balance the now-unbalanced magnetic fields, which gives you two smaller magnets with a north and south pole each. 

Wikipedia already had a good picture of what happens when you break a magnet, saving me countless minutes of MSPaint work.

As classical physics goes, you're not going to get much more useful than Maxwell's equations (see below).  Depending on how you solve them, they can tell you everything from how circuits work to how a cell phone signal will propagate from a tower.  In other words, they basically predict everything that has to do with electricity and/or magnetism, and for the most part they do it really accurately.  So when they say something like a magnetic monopole is a physical impossibility, I'm generally inclined to buy it.

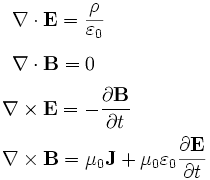Maxwell's equations.  Like the DMV, they are a total pain in the ass but it's almost impossible to avoid dealing with them at some point, at least if you're doing science.

You know who was way less lazy than me (and also probably smarter)?  Paul Dirac.  He was one of the handful of geniuses who made everybody's lives more difficult by developing quantum mechanics in the mid-20th century.  Quantum mechanics is horrendously complicated but easy to sum up: when shit gets small, shit gets weird.  In other words, when you start thinking at the scale of atoms and molecules, normal physics goes out the window and you get things like electrons passing through solid barriers and particles randomly popping in and out of existence happening as a matter of routine.  On the macroscopic scale this doesn't affect us a whole lot (which is why it took so long for anyone to even realize quantum mechanics was a thing), but it's turned out to be pretty important anyway (transistors, for example, shouldn't work according to strict classical physics, but they definitely do).

Dirac worked out that, at the quantum level (where things like matter and energy are quantized into discrete, indivisible chunks, hence the name), the rules for magnetic fields might be a bit different.  The math on the Wikipedia page is currently making my head hurt and I'm not even going to pretend I understand or can verify it, but the upshot of Dirac's result is that, if electric charge is quantized (it is) and Maxwell's equations have basically the correct form (they do), then it should be possible for nonzero magnetic charge (magnetic monopoles, in other words) to exist.  Since we know that electric charge is quantized (because you can't ever have less than one electron's worth of charge) then the implication is that, contrary to all common sense, magnetic monopoles are a thing, at least at the subatomic scale (at the macro scale, electrons are small enough that you can't really treat charge as quantized, like how you don't think of a glass of water as being made up of a shitload of hydrogen and oxygen atoms).  Subsequent work in even more advanced physics that I'm even less qualified to comment on appears to also support the existence of monopoles, generally in the form of subatomic particles with a discrete magnetic charge that would be almost exactly analogous to electrons. 

So (very tiny) magnetic monopoles CAN exist.  That's a long way from saying that they DO exist, let alone that they exist outside a cryogenic vacuum chamber or supercollider or something.  So far, pretty much all attempts to detect a subatomic-sized magnetic monopole, using everything from SQUIDs (the most sensitive magnetic-field detectors ever built) to the Large Hadron Collider that's currently getting so much publicity for all that Higgs boson business, have been failures.  There have been a couple of blips, but nothing anyone's been able to reproduce.  This has led to the general consensus that, if they do exist, they're extremely rare and/or hard to detect even under weird, artificial conditions like the inside of a giant particle accelerator or the near-absolute-zero temperatures a SQUID operates at. 

This was all pretty disappointing to an electrical engineer like myself, whose general ignorance of advanced physics led to thoughts of macro-scale magnetic monopoles existing somewhere just waiting to be mined, and more thoughts of the weird gadgets and motors and things you could build with them (to be fair, I think I got most of that idea from a Larry Niven short story).  Unfortunately the fact that, if they're around at all, monopoles only exist as nearly undetectable subatomic particles kind of limits their usefulness for basically everything, except proving this or that formulation of string theory is a little more plausible, if they're ever detected.  When someone figures out how to generate a focused beam of magnetically-charged particles I'll get excited and/or think of something cool to do with it; until then the eggheads can keep them.